Notice
Recent Posts
Recent Comments
Link
변수의 기록
(코테) 백준_2512_예산 *이분 탐색 (Binary Search) 본문
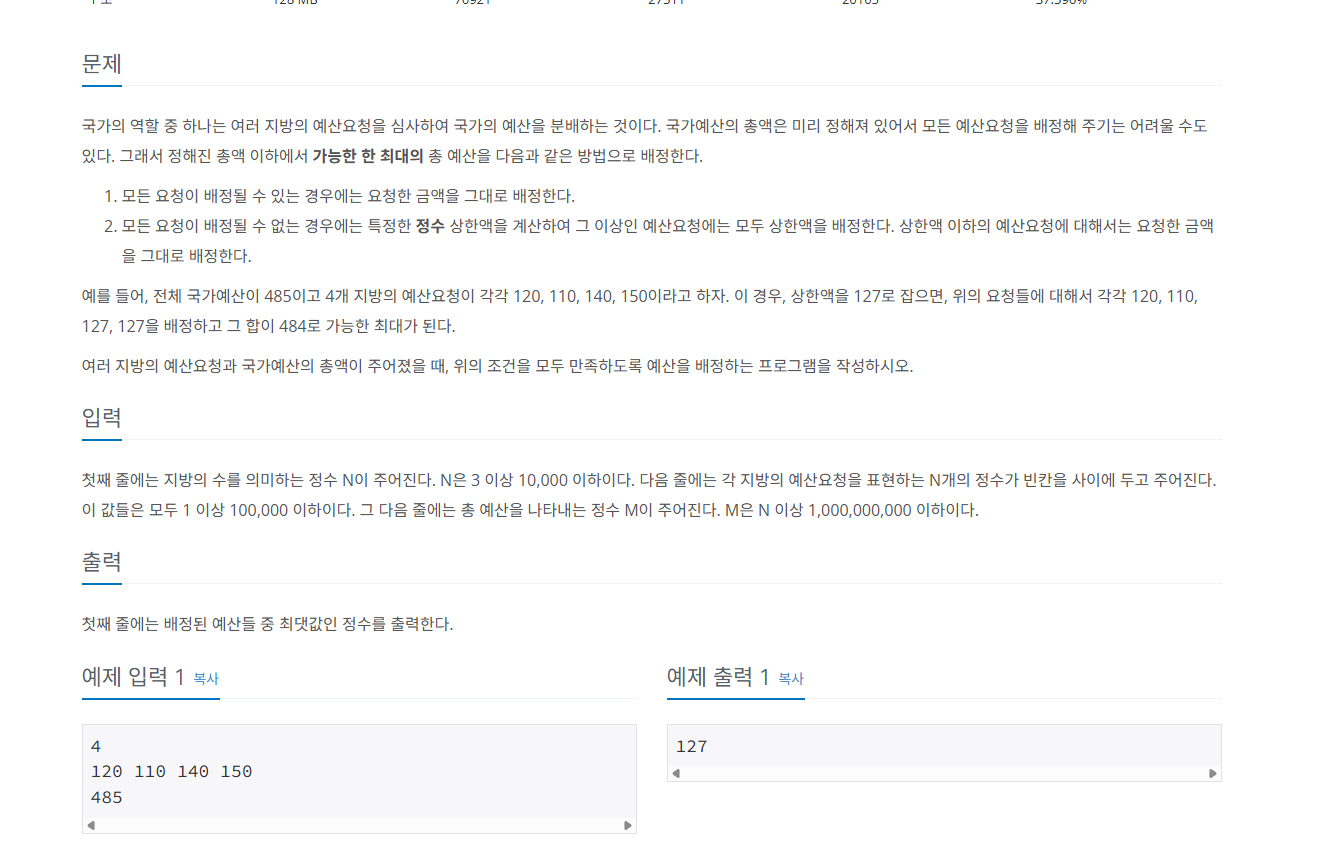
내가 제시한
package test;
import java.util.*;
import java.io.*;
public class Backjun_2512 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//첫쨰줄 값 세팅 (지방 개수)
int N= Integer.parseInt(br.readLine());
int[] list = new int[N]; ;
//둘쨰줄 값 세팅 (지방에서 제시한 값 리스트)
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0;i<N;i++) {
list[i] = Integer.parseInt(st.nextToken());
}
//셋째줄 값 세팅 (세액 가능 총액)
int T =Integer.parseInt(br.readLine());
int left = 1;
int right = Arrays.stream(list).max().getAsInt();
int result = 0;
//종료까지 반복
while(left<=right){
int mid=(left+right) / 2; //상한가
long sum =0;
for(int i=0;i<N;i++){
//평균치보다 높아? 그럼 평균치로 해
if(mid<list[i]){
sum += mid ;
}else{ //평균치보다 안높아? 그럼 너값으로해
sum += list[i];
}
/* 최적화 코드 (결국 작은 값을 sum 하는거니)
for (int value : list) {
sum += Math.min(value, mid);
}
*/
}
//합= T보다 넘침
if(sum>T){ //오른쪽 값 줄여 (가능한 총액 초과함)
right = mid-1;
}else{ //왼쪽 값 늘려 (가능한 총액 미달 혹은 동일 더 상한가 올려보자)
result = mid; //상한가 최신화
left = mid+1;
}
}
System.out.println("");
System.out.print(result);
}
}
위 문제 백준 2512번 (시간 복잡도)
- N: 지방의 개수 (최대 10,000)
- 요청 금액 최대값: 최대 100,000 (right)
- 이분 탐색 구간: 0 ~ max(requests) → 최대 100,000번까지 가능- 이분 탐색 횟수: log₂(max 요청 금액) → 약 log₂(100,000) ≒ 17
- 각 탐색마다 sum 계산: 배열 전체 순회 → O(N)
⏱ 최종 시간 복잡도 = O(N × log M)
- N: 배열 크기 (최대 10,000)
- M: 요청 금액의 최댓값 (약 100,000)
⇒ 대략 O(10,000 × 17) = 170,000 → 충분히 빠름✅ 이분 탐색 시간복잡도 순위표 (간단 정리)
| 분류 | 알고리즘 | 시간 복잡도 |
| ✅ 빠름 | 이분 탐색 | O(log N) |
| ✅ 빠름 | 파라메트릭 서치 (+배열 탐색) | O(N log M) |
| 보통 | 정렬 | O(N log N) |
| 보통 | DFS / BFS | O(N + E) |
| 느림 | 브루트포스 | O(2^N), O(N!) 등 |
회고.
지난번 이분탐색 관련 문제를
완전탐색? (브루트포스) 로 풀어 O(2^n) 으로 풀었으나,
이분 탐색 (Binary Search) 알고리즘을 학습한 후 적용하여 O (N log M ) 의 시간복잡도로 해결하였다.
'기타 > 코딩테스트' 카테고리의 다른 글
| (코테) 백준_1717_집합의 표현 *유니온 파인드 (0) | 2025.05.29 |
|---|---|
| (코테) 백준_2110_공유기 설치 *이분탐색 (0) | 2025.05.28 |
| (코테) 백준_1654_랜선 자르기 *이분 탐색 (0) | 2025.05.27 |
| (코테) 백준_15661_링크와 스타트 *백트레킹 , 비트마스킹 + 브루트포스 코드 (0) | 2025.05.26 |
| (코테) 백준_유형별 풀이 파악하는 팁 (0) | 2025.05.24 |





