레드-블랙 트리(Red-Black Tree) 개념과 속성 정리
레드-블랙 트리는 자기 균형 이진 탐색 트리(Self-balancing BST) 의 일종이다. 일반 이진 탐색 트리(BST)는 삽입 순서에 따라 한쪽으로 편향될 수 있는데, 레드-블랙 트리는 특정 규칙을 통해 항상 트리의 높이를 O(log N) 수준으로 유지함으로써 검색, 삽입, 삭제 연산을 효율적으로 만든다.
✅ 기본 개념
- 이진 탐색 트리(BST)의 변형으로, 추가적인 색상 속성을 가지는 트리.
- 모든 노드는 Red 또는 Black 색을 가짐.
- 자체적으로 균형을 유지하여, 최악의 경우에도 탐색 시간이 O(log N)을 보장함.
✅ 레드-블랙 트리의 5가지 주요 속성
- 모든 노드는 Red 또는 Black이다.
- 루트 노드는 항상 Black이다.
- 모든 leaf 노드(NIL 노드)는 Black이다.
- 실제 값이 없는 NIL 노드는 트리의 균형 계산에 사용됨.
- Red 노드의 자식은 모두 Black이다.
- 즉, Red 노드가 연속적으로 나타날 수 없다.
- 임의의 노드에서 그 자손인 모든 NIL 노드로 가는 경로에는 같은 수의 Black 노드가 있다.
- 이를 Black Height라고 부르며, 균형 유지의 핵심 조건이다.
✅ NIL 노드란?
- 실제 데이터가 존재하지 않는 leaf 자리에 존재하는 가상 노드.
- 모든 leaf 노드 자리에 존재하며, 색은 Black.
- 균형 계산(Black Height)에 포함되므로, 트리 구조 상 매우 중요.
✅ Black Height란?
- 어떤 노드 X에서 그 자손 NIL 노드까지 가는 경로 중 포함된 Black 노드의 개수 (X 자신은 포함하지 않음).
- 모든 경로의 Black Height는 동일해야 하며, 이는 속성 #5의 내용이다.
✅ 삽입 시 기본 규칙
- 삽입되는 노드는 항상 Red로 시작한다.
- 삽입 직후에는 Red-Black 트리의 속성 중 일부가 깨질 수 있기 때문에, 색상 재조정과 회전(Rotation) 을 통해 균형을 복구한다.
✅ 삽입 시 발생할 수 있는 3가지 주요 경우와 해결 방식
Case 1: 부모와 삼촌이 모두 Red인 경우
- 조치:
- 부모와 삼촌을 Black으로 변경
- 할아버지를 Red로 변경한 후
- 할아버지를 기준으로 다시 검증을 재귀적으로 수행
Case 2: 부모는 Red, 삽입된 노드가 부모의 반대 방향에 있을 때 (Zig-Zag 구조)
- 예: 부모가 왼쪽 자식, 삽입 노드는 부모의 오른쪽 자식
- 조치:
- 부모를 기준으로 회전하여 Case 3으로 변환
- 그 후 Case 3 방식으로 처리
Case 3: 부모는 Red, 삽입 노드가 부모와 같은 방향 (Zig-Zig 구조)
- 예: 부모가 왼쪽 자식, 삽입 노드도 왼쪽 자식
- 조치:
- 부모와 할아버지의 색을 교체
- 할아버지를 기준으로 회전 (예: 왼쪽-왼쪽 구조 → 오른쪽 회전)
✅ 삽입 처리에서 핵심은 레드-레드 연결을 제거하고, Black Height를 유지하는 것이다.
✅ 회전(Rotation)
- BST 속성을 유지하면서 트리의 균형을 맞추는 구조 변경 기법
- 두 가지 종류:
- Left Rotation: 노드를 왼쪽으로 끌어올림
- Right Rotation: 노드를 오른쪽으로 끌어올림
- 삽입 또는 삭제 후 속성 위반 시 사용됨
예제
레드- 블랙 트리 삽입 예제
1. '40' insert

1-1 변경
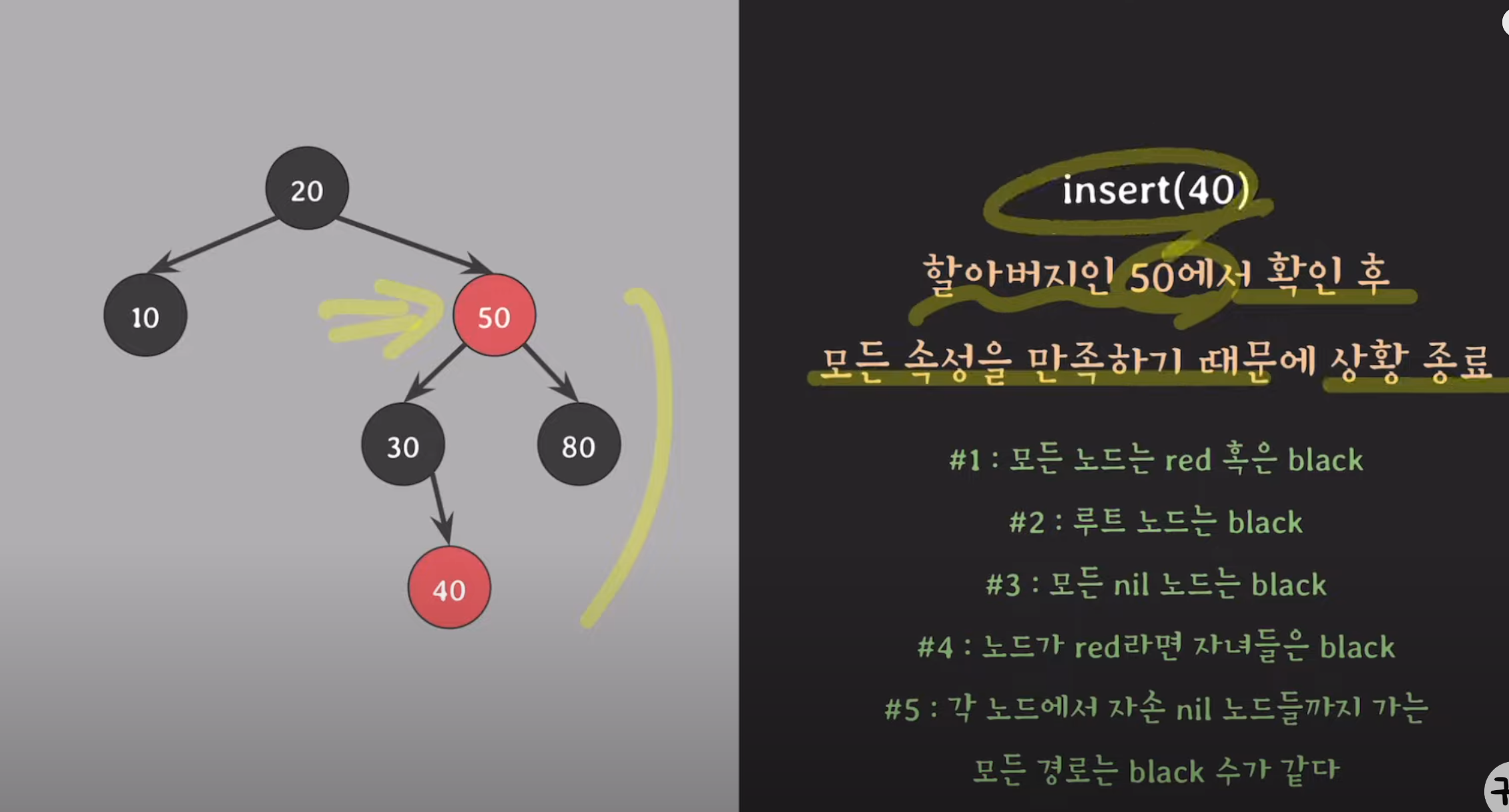
-------------------------------------------------------------------------------------------------------------------------------------------------------------
2. '35' insert
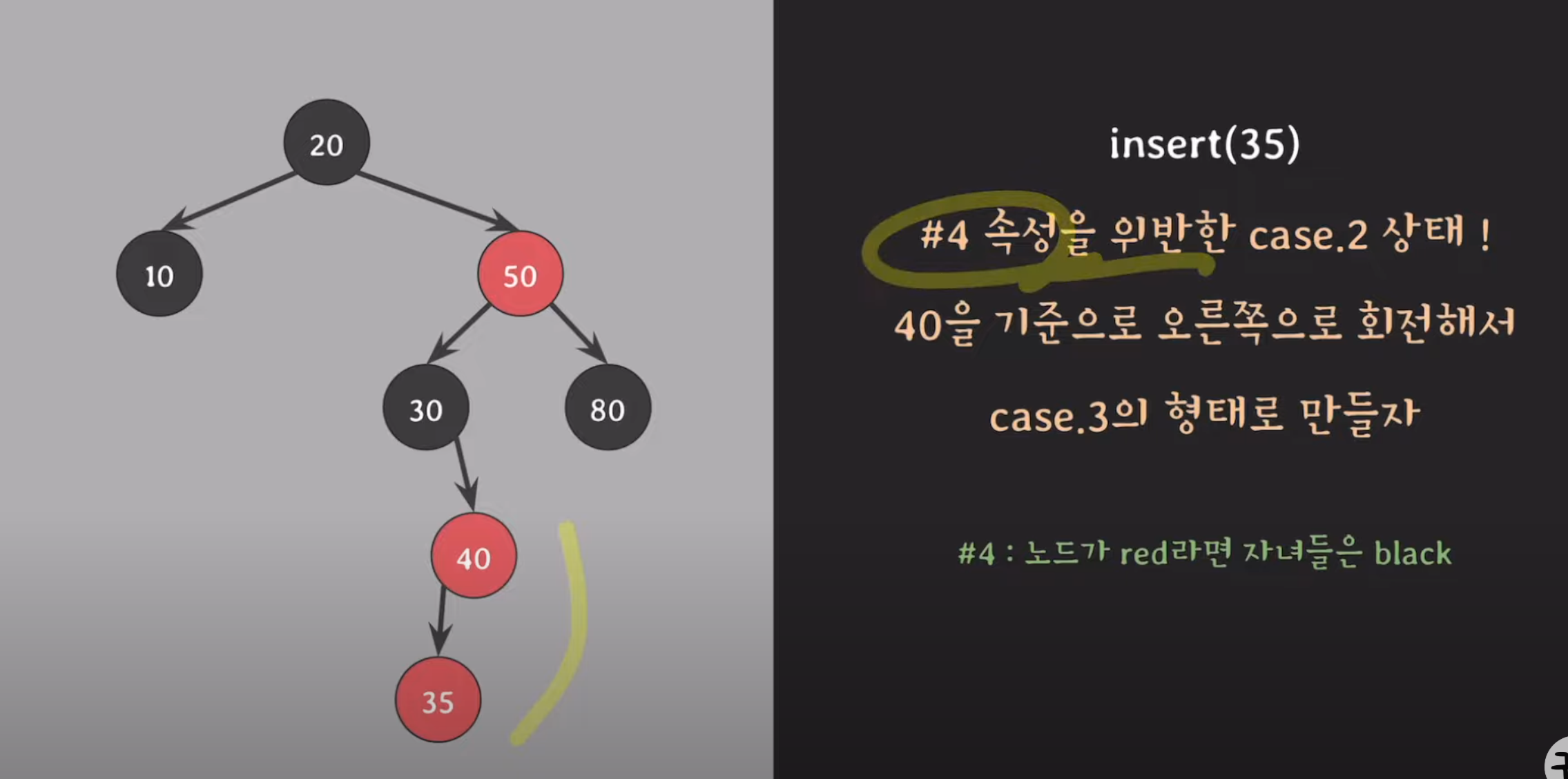
2-1 회전을 통해 case 2 상태 해결
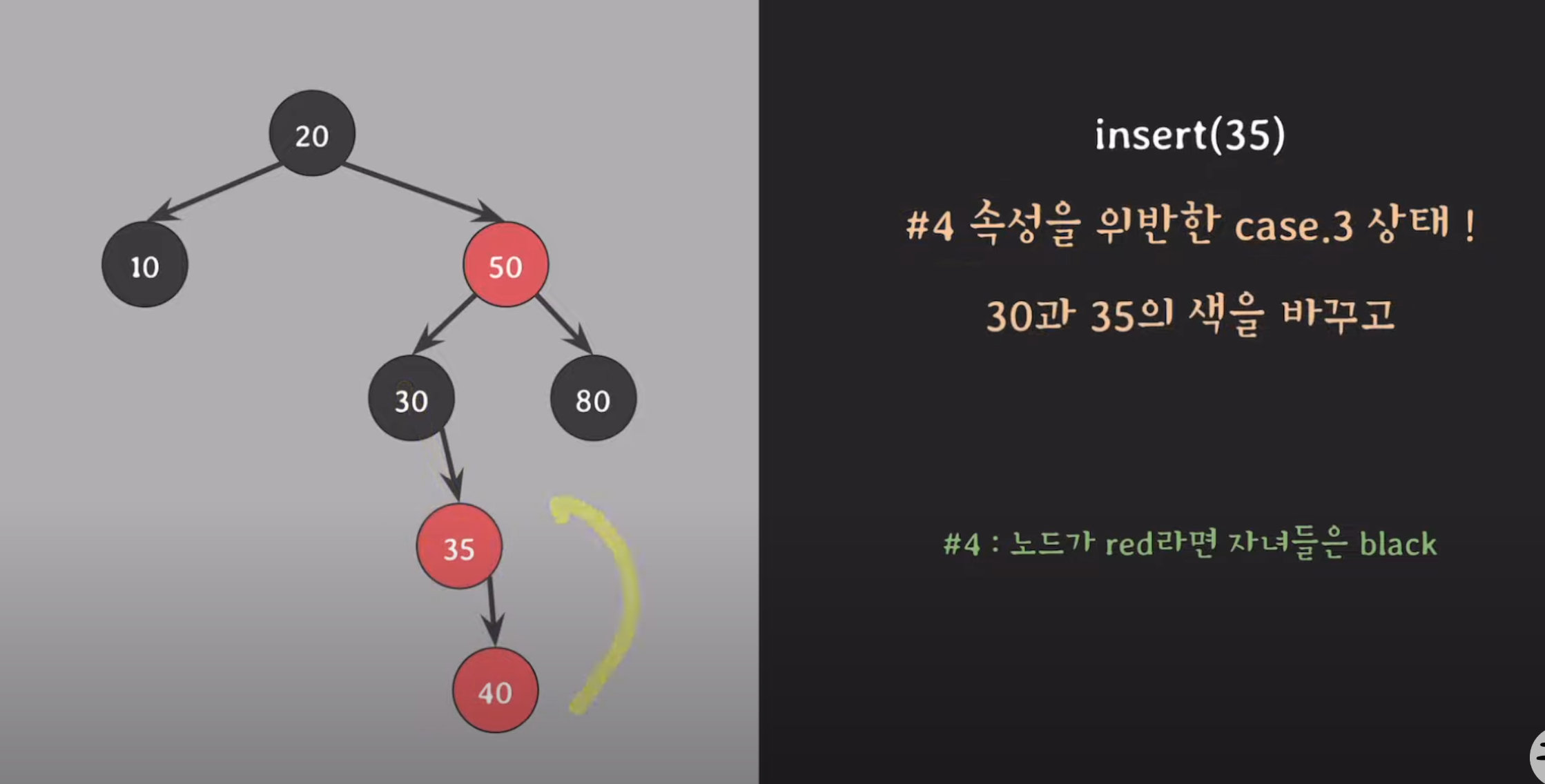
2-2 30 <-> 35 색 변경
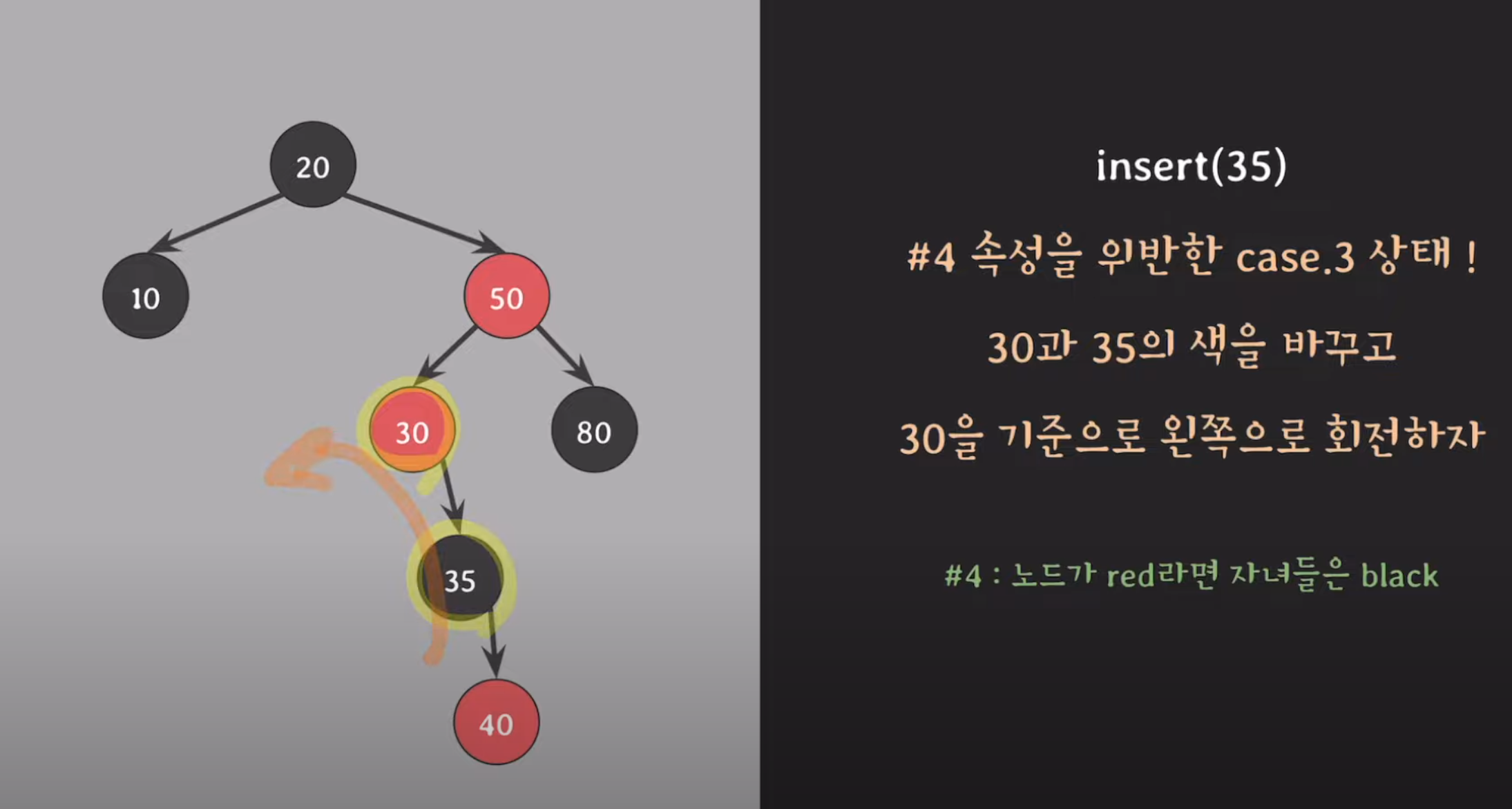
2-3 왼쪽으로 회전 해서 해결
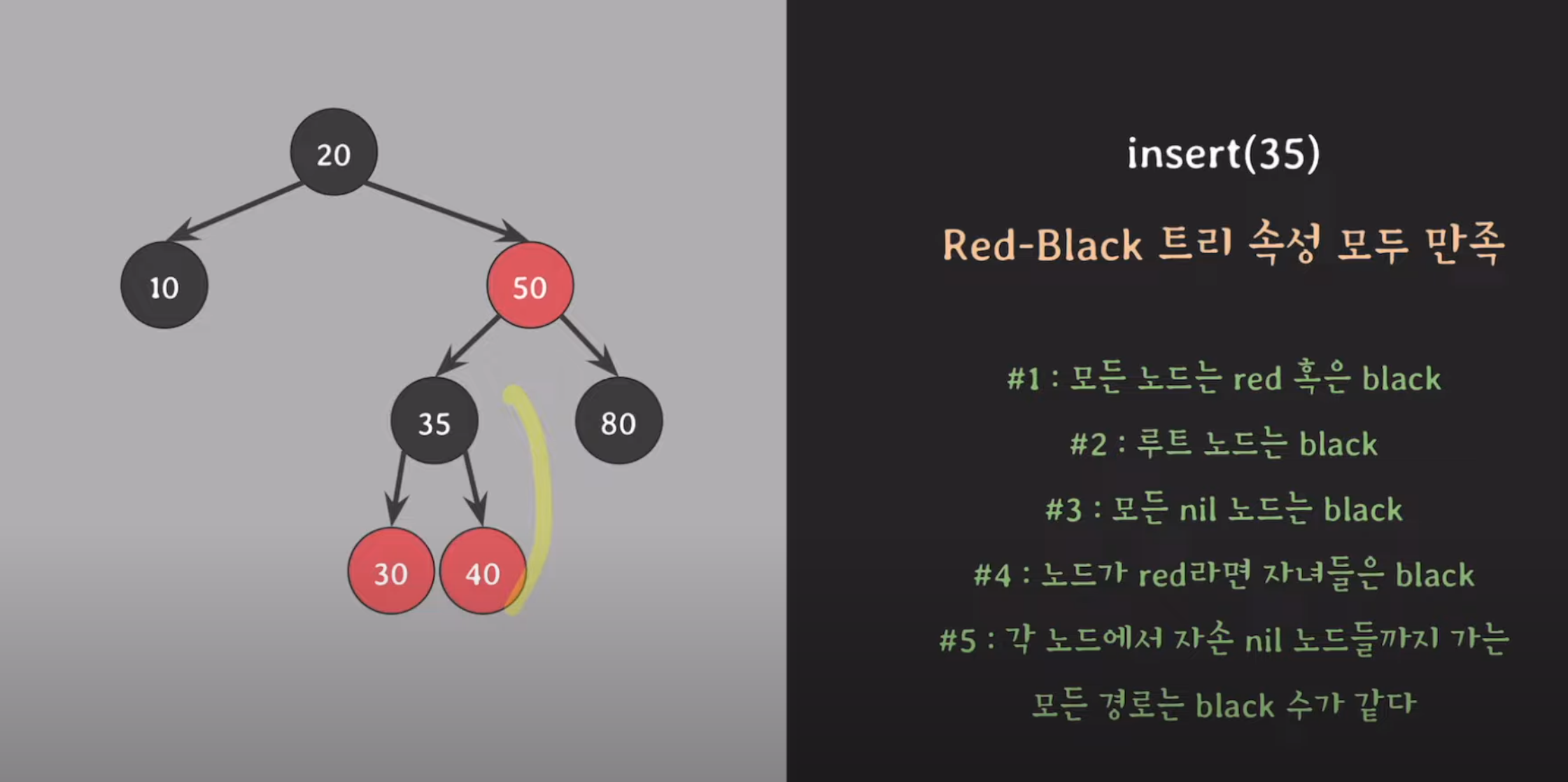
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
3. '25' insert
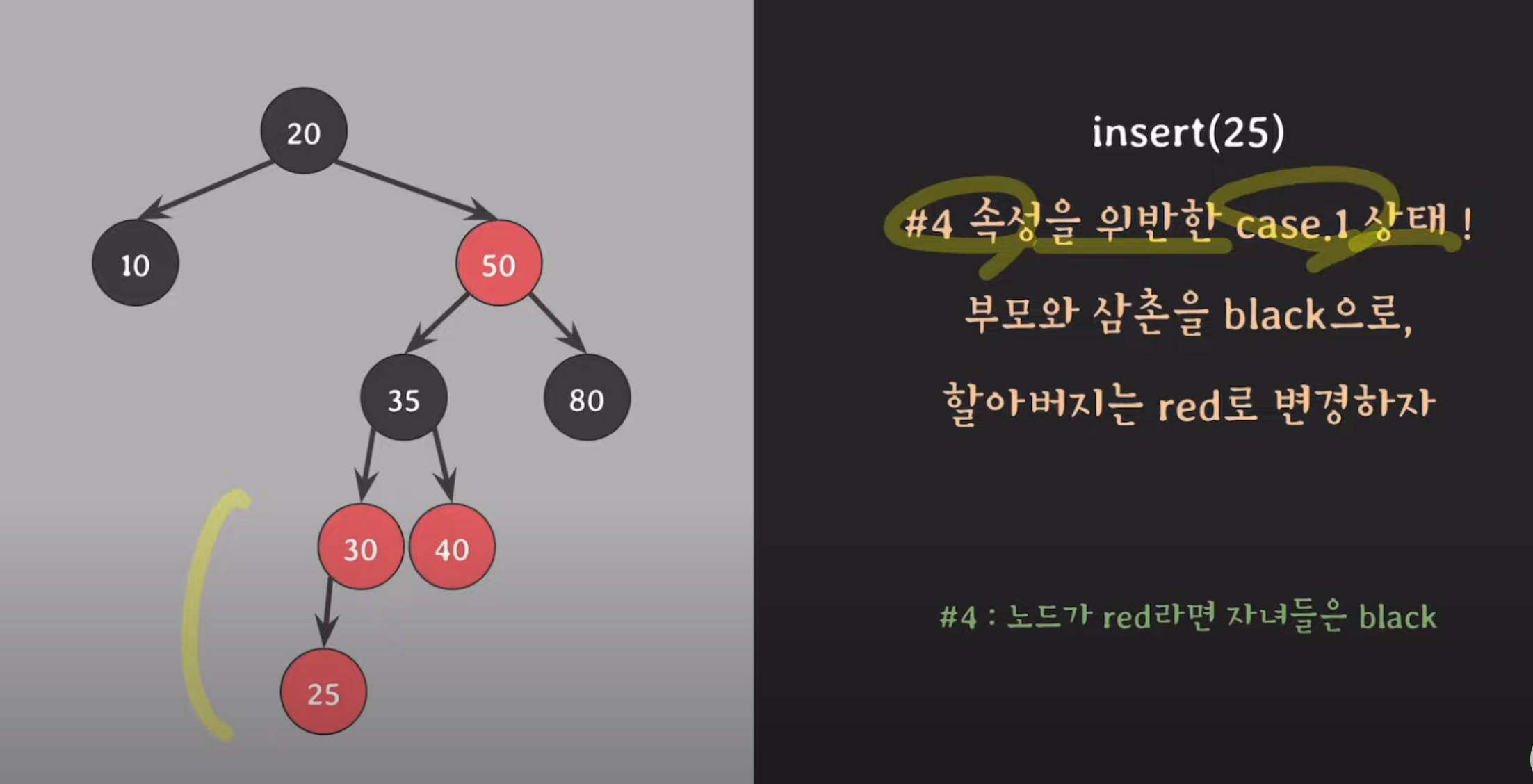
3-1. case1 해결 위해 할아버지 <-> 부모,삼촌 색 변경
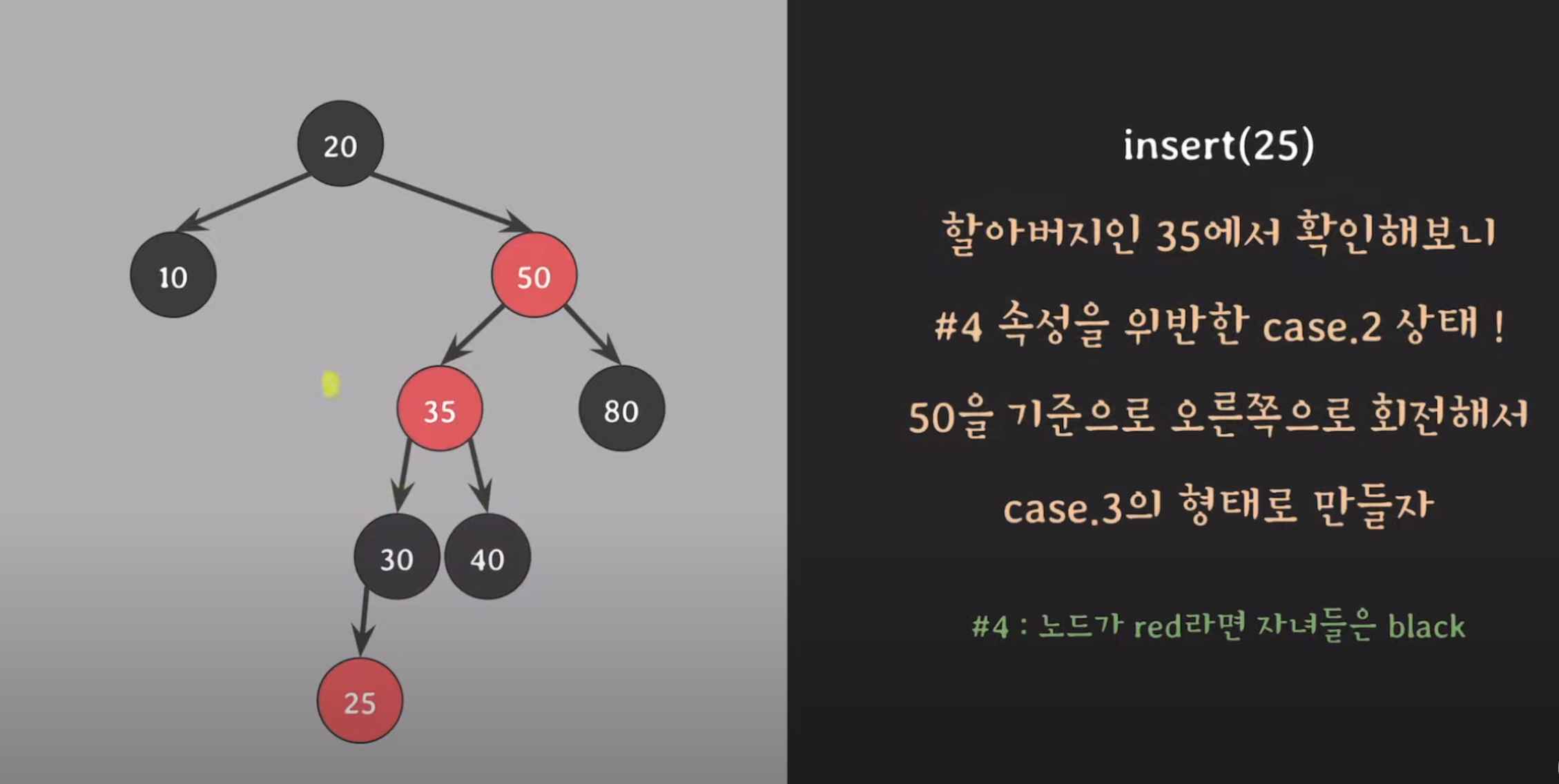
3-2. 오른쪽 회전을 통해 case3 상태로 변경

3-3. 20 <-> 35 색 변경

3-4. 35를 루트로 위로 올려줌.

✅ 참고 정리
- Red-Black 트리는 AVL 트리보다 약간 느릴 수 있으나, 회전 수가 적기 때문에 삽입·삭제 성능이 우수한 편.
- 트리 높이는 최대 2 * log(N) 이내로 제한됨.
*사진 출처 - 유튜브 쉬운코드
'CS지식 > 자료구조 (Data Structure)' 카테고리의 다른 글
| (자료구조) 코딩테스트 자주 나오는 자료구조 총정리 (Java 기준) (0) | 2025.06.22 |
|---|---|
| (자료구조) 레드-블랙(red-black) 트리의 삭제 동작 방식과 시간복잡도 PART2 (예제 포함!!!!!) (0) | 2025.05.02 |
| (자료구조) AVL 트리 개념과 특징 (0) | 2025.04.30 |
| (cs)이진 탐색 트리 (Binary Search Tree, BST) (1) | 2025.04.27 |
| 트리(Tree) 기본 구조와 핵심 개념 정리 (0) | 2025.04.27 |