CS지식/자료구조 (Data Structure)

(자료구조) AVL 트리 개념과 특징

불광동 물주먹 2025. 4. 30. 00:50

AVL 트리 개념과 특징

1. AVL 트리란?

AVL 트리는 **이진 탐색 트리(BST)**의 일종이다.
스스로 균형을 잡는(self-balancing) 특성을 갖는다.
1962년 Georgy Adelson-Velsky와 Evgenii Landis가 고안했다. (AVL 이름 유래)

2. AVL 트리의 핵심: 밸런스 팩터 (Balance Factor)

임의의 노드 X에 대해 밸런스 팩터(BF)는 다음과 같이 정의한다.

BF(X) = 높이(왼쪽 서브트리) - 높이(오른쪽 서브트리)
AVL 트리의 모든 노드는 반드시 다음 중 하나의 BF 값을 가진다.

BF ∈ {-1, 0, 1}

이 범위를 벗어나면 트리의 균형이 깨진 것으로 판단하여 **균형 조정 작업(회전)**을 수행한다.

사진 출처 - 유튜브 쉬운코드

AVL 트리 균형 잡기 메커니즘

AVL 트리는 삽입 또는 삭제 연산 이후 다음 과정을 통해 스스로 균형을 유지한다.

삽입(Insert) 시

새 노드를 일반 BST 방식으로 삽입한다.
삽입한 노드에서 부모 방향으로 올라가면서 각 노드의 BF를 갱신한다.
만약 어떤 노드의 BF가 {-1, 0, 1}을 벗어난다면, 그 지점을 기준으로 **회전(rotation)**을 수행하여 균형을 맞춘다.

삭제(Delete) 시

삭제할 노드를 일반 BST 방식으로 찾고 삭제한다.
삭제한 노드의 부모 방향으로 올라가며 각 노드의 BF를 갱신한다.
역시, BF가 {-1, 0, 1}을 벗어나는 순간 회전을 수행하여 균형을 맞춘다.

루트 노드 삭제 시

루트의 값을 삭제할 경우, 일반적으로 오른쪽 서브트리에서 가장 작은 값(또는 왼쪽 서브트리에서 가장 큰 값)을 찾아 대체한다.
이후 다시 AVL 조건을 만족하도록 균형 조정한다.

사진 출처 - 유튜브 쉬운코드

루트 삭제 후 결과 값

사진 출처 -유튜브 쉬운코드

AVL 트리의 회전 (Rotation)

트리 균형이 깨졌을 때 사용되는 조정 방법이다.

1. LL 회전 (Left-Left)

왼쪽 자식의 왼쪽 서브트리에 삽입/삭제로 인해 균형이 깨진 경우
해결: 오른쪽으로 단순 회전

오른쪽 회전 후

2. RR 회전 (Right-Right)

오른쪽 자식의 오른쪽 서브트리에 삽입/삭제로 인해 균형이 깨진 경우
해결: 왼쪽으로 단순 회전

3. RL 회전 (Right-Left)

오른쪽 자식의 왼쪽 서브트리에서 삽입/삭제로 인해 균형이 깨진 경우
해결: 오른쪽 회전 후 왼쪽 회전(2번 회전)

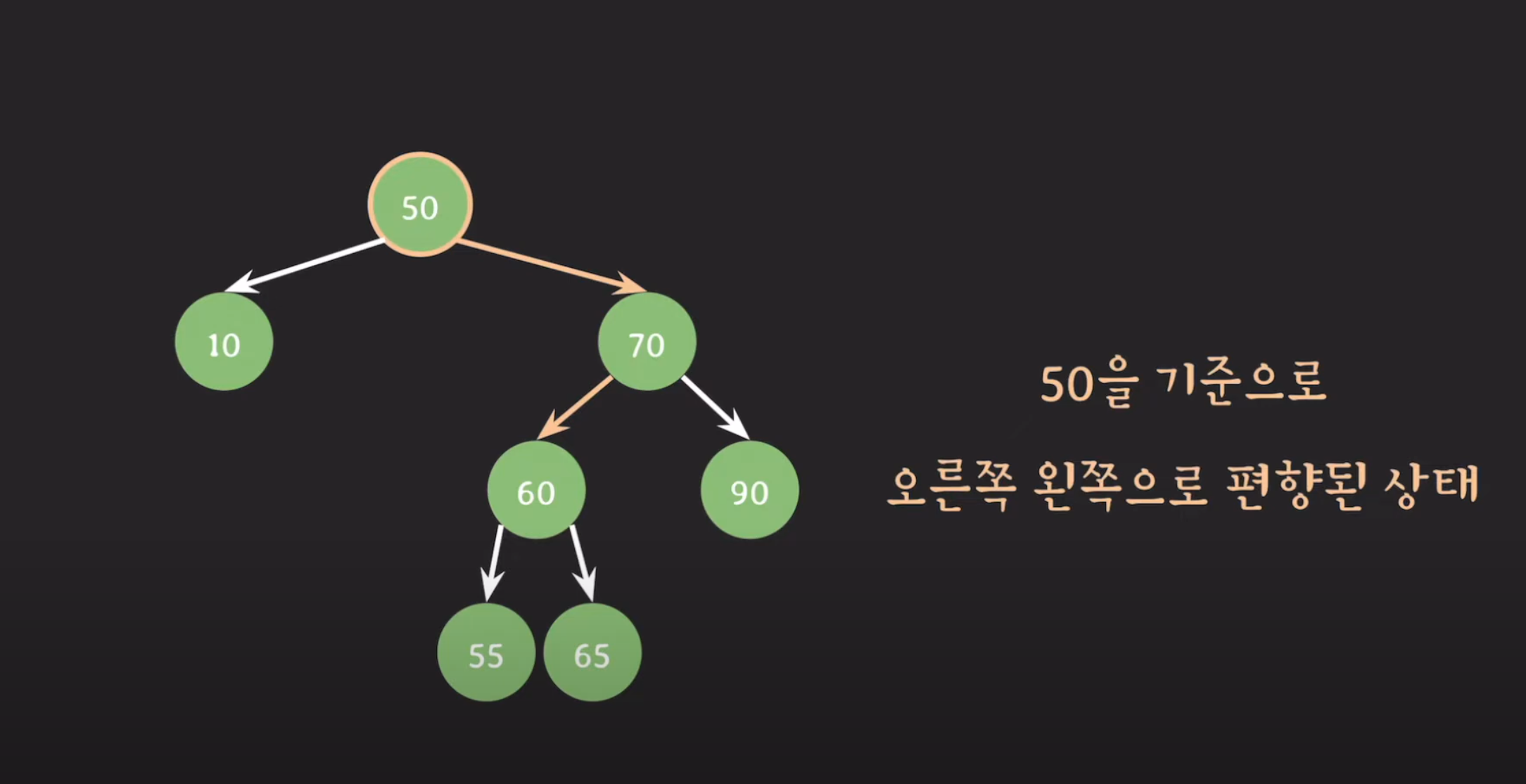
조정 후

4. LR 회전 (Left-Right)

왼쪽 자식의 오른쪽 서브트리에서 삽입/삭제로 인해 균형이 깨진 경우
해결: 왼쪽 회전 후 오른쪽 회전(2번 회전)

※ 핵심: 트리 편향 방향에 따라 필요한 회전 방향이 달라진다.

AVL 트리의 시간 복잡도

📊 AVL 트리 시간 복잡도 정리표

연산 종류	최선 (Best)	평균 (Average)	최악 (Worst)
삽입 (Insert)	Θ(1)	O(log N)	O(log N)
삭제 (Delete)	Θ(1)	O(log N)	O(log N)
탐색 (Search)	Θ(1)	O(log N)	O(log N)

※ AVL 트리는 항상 거의 완벽한 균형을 유지하므로 높이(height)가 O(log n)에 제한된다.

AVL 트리의 장점과 단점

장점

탐색이 빠르다. 항상 log n의 깊이를 보장하기 때문에 검색 효율이 매우 좋다.
엄격한 균형 유지. 균형이 잘 맞춰져 있어 최악의 경우에도 탐색/삽입/삭제 시간 복잡도가 보장된다.

단점

삽입/삭제 비용이 크다.
노드 삽입/삭제 시 매번 BF를 갱신하고 필요하면 회전을 수행해야 하므로 성능 부담이 있다.
구현 복잡성.
단순한 BST에 비해 구현이 복잡하고, 디버깅 난이도도 높다.

AVL 트리의 한계와 대안

AVL 트리는 엄격한 균형 유지로 인해 삽입/삭제가 빈번한 경우 부담이 크다.
그래서 실무에서는 약간 균형을 느슨하게 유지하더라도 성능 최적화된 트리를 사용하는 경우가 많다.
대표적인 예가 Red-Black 트리이다. (AVL보다 삽입/삭제가 빠르고 효율적임)

요약

AVL 트리는 엄격하게 균형 잡힌 이진 탐색 트리다.
Balance Factor를 기준으로 삽입/삭제 후 균형을 유지한다.
균형이 깨지면 회전을 통해 스스로 조정한다.
탐색은 빠르지만, 삽입/삭제는 비용이 더 든다.
실무에서는 경우에 따라 Red-Black 트리 같은 대안 구조도 고려한다.